
PY 131 Chapter 8: Rotational Motion
Center of Mass
So far we have been treating all objects as point masses.
For every real object or system of objects, there is a point called the Center of Mass CM, which moves as if all the mass of the object were located there.
the CM does not have to be inside the object
Consider a system made from two point masses mA and mB placed along the x axis at xA and xB .
The total mass is
M=mA+ mB
The CM for the system is defined to be
x_CM = (m_A/M)(x_A) + (m_B/M)(x_B)
For a system of many point masses, x_CM is the weighted average of the x coordinate of each point mass.
This can be generalized to point masses, not along a line – the same formula applies to the y and z coordinates.
Consider three equal masses which form a triangle. The coordinates of the CM are the weighted average of their x and y coordinates.
Motion of the CM
Consider a system made up of two or more objects.
Their masses can all be different.
The total mass of all the objects is M.
The correct form for Newton’s Second Law is
a_CM = 1/M(F_ext)
Where Fext is the net external force on the system.
An external force is one that comes from something outside the system
If two objects in the system exert forces on each other, those are internal forces and do not contribute to Fext.
The center of mass moves like a point particle with mass M under the net external force acting on the system.
Rotational Motion
In addition to translational motion, objects which are not points, and systems of objects, can rotate.
We shall consider only rigid objects (rigid bodies) which have a fixed shape.
For now, the rotation is around a single line in space called the axis of rotation.
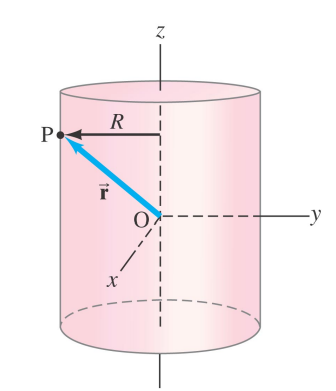
Polar Coordinates
Every point in the object moves in a circle.
Point P has coordinates x,y,z and is a distance r from the axis.
At time t the position vector makes an angle θ with the x axis.
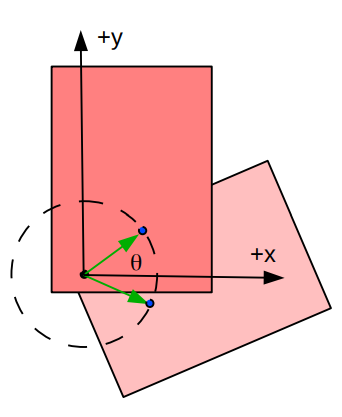
Because the motion is circular the coordinates x and y are not very useful.
The more useful coordinates are the polar coordinates r and θ.
Angular Velocity
At time t_1 the angle is θ1 , at time t 2 the angle is θ2.
The average angular velocity ω is defined to be
ω¯= change in angle/change in time = (θ2−θ1)/(t 2−t 1) = Δθ/Δ t
The SI units of ω are radians/s (rad/s).
By convention, if ω is positive the rotation is counterclockwise (CCW), if it is negative the rotation is clockwise (CW).
When the time interval approaches zero the average angular velocity becomes the instantaneous angular velocity ω.
Period and Frequency
In one period T the object completes one revolution i.e. it rotates through 2π radians.
If the angular velocity is constant then ω = ω.
ω= Δ θ / Δ t = 2π / T
The frequency f is the inverse of the period T.
f = 1 / T
Angular Acceleration
At time t_1 the angular velocity is ω1 , at time t 2 the angular velocity is ω2.
The average angular acceleration α is defined to be
α¯= change in angular velocity / change in time = (ω2−ω1)/ (t 2−t 1) = Δ ω / Δt
The SI units of α are rad/s^2.
When the time interval approaches zero the average angular acceleration becomes the instantaneous angular acceleration α.
Any point in the object still has a linear (tangential) velocity, speed and acceleration.
The velocity vector always points along the tangent to the circle.
If the distance of the point is r from the axis then the linear speed is
v=r×ω
In a rigid object the tangential speed increases with distance from the axis of rotation.
The circumference of the circle grows but the period does not.
An object moving in a circle is accelerating.
The acceleration is related to the angular acceleration and angular velocity.
The general relation is complicated because in general there are two components of the acceleration.
One points towards the center and is called the centripetal acceleration aC
The centripetal acceleration causes the velocity to change direction only.
The other points in the same direction as the velocity (or opposite it) and is called the tangential acceleration, a_tan.
The tangential acceleration changes the size of the velocity (speed) only.
They are related to ω and α by the equations.
a_C=r×ω^2 = v^2/r
a_tan =r×α
In the special case where a_tan is zero, the acceleration points towards the center of the circle, and the object’s speed is constant.
This kind of motion is called uniform circular motion.
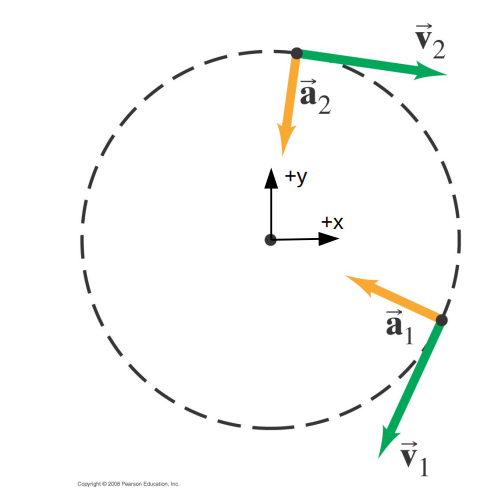
In general the acceleration points in a non-central direction. This kind of motion is called non-uniform circular motion.

Centripetal Force
The centripetal acceleration occurs due to the application of a force called the centripetal force.
Typically the force is a tension in a string, gravity, or a normal force, it is not some new force in the problem.
Since we know the centripetal acceleration, the force must be:
∑ _radial components F= FC=maC= mv^2 / r =mrω^2
The sum is over the radial components of the applied forces.
If an applied force has no radial component then it doesn't contribute.
If the component points towards the axis of rotation it is positive, away from the axis of rotation it is negative.
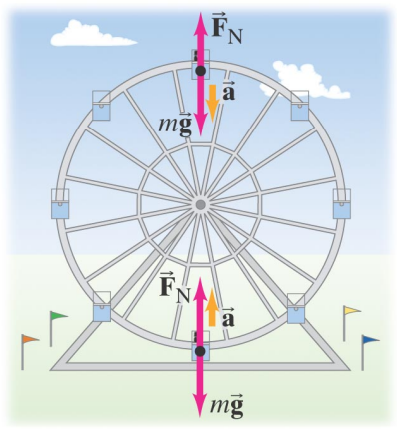
A rider on a Ferris wheel moves in a vertical circle of radius r at constant tangential speed v.
How does the normal force that the seat exerts on the rider change compared to the rider’s weight at the top and bottom of the wheel?
Another common instance of circular motion occurs when a car rounds a curved road.
The centripetal force – the force that causes the car to follow the curved road – is friction and/or the normal force if the road is banked.
if the wheels are not skidding then the point on the tire in contact with the ground is not moving plus the friction is perpendicular to the motion so the appropriate friction to use is static friction, not kinetic or rolling.
Centrifugal Force
In the frame of reference of an object moving in a circle, there is a force pushing on the object in the outward direction
This force is called the centrifugal force.
The centrifugal force is an example of a fictitious force – a force that is only felt in an accelerating frame of reference.
It is equal in size to the centripetal force.
The centrifugal force is why astronauts on the space station feel weightless – the centripetal force is their weight so in the frame of reference of the space station (which is also accelerating) the centrifugal force is equal and opposite their weight.
Torque
To make an object rotate – or change how it is rotating – we have to apply a force.
The larger the force the more rapidly the change in rotational motion of the object.
The effectiveness of the force increases with the distance from the axis of rotation.
The force is more effective if it is applied perpendicular to the vector from the axis to the point of application.
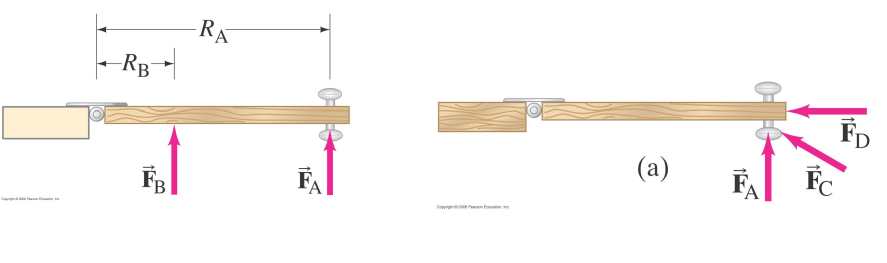
These observations indicate the relevant property is not force itself but the product of the size of the force, the distance from the rotation axis, and the angle the force is pointing.
This product is called the torque and usually represented by τ.
Torque is not exactly a vector but it has many properties of a vector e.g. it adds like all vectors do
If a torque tries to rotate an object in a CCW sense, it is positive.
If a torque tries to rotate an object CW it is negative.
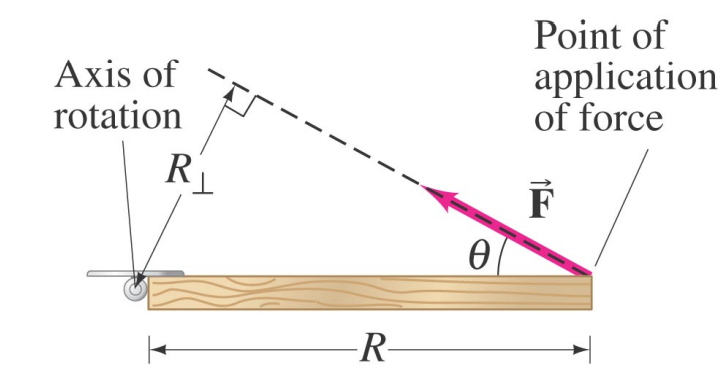
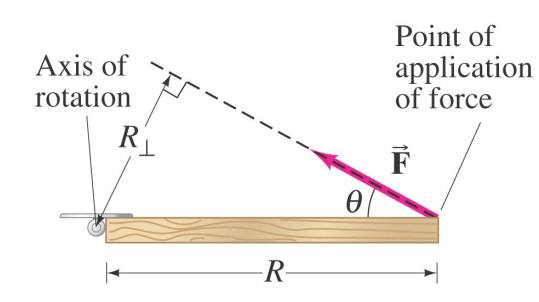
Consider a force applied to an object which can rotate, at a particular point.
The force vector defines a line through space.
The lever arm is the shortest distance from the axis of rotation to that line.
The torque of the force is
τ=R⊥ F
The Moment of Inertia
The moment of inertia I plays the roll of mass for rotational motion.
The larger the moment of inertia the harder it is to change the angular velocity of a rotating object.
The moment of inertia for a point mass going around a circle with radius r is
I=mr^2

For a hoop, a disc and a sphere all of the same mass and radius, the moment of inertia of the hoop is largest, then the disc, then the sphere.
Newton’s Law of Fixed Axis Rotation
Newton's laws (in a modified form) also apply to fixed axis rotation.
Every object continues in its state of rest, or of uniform angular velocity, as long as no net torque acts on it.
The angular acceleration of an object about some axis is directly proportional to the net torque acting on it about that axis, and is inversely proportional to the object's moment of inertia I about that axis.
α= 1/I (τ_net)
Whenever one object exerts a torque on a second object, the second exerts an equal torque in the opposite direction on the first.
Kinetic Energy of Rotation
The kinetic energy of a single point mass is
Ktrans =½mv^2
If the point mass is going around in a circle of radius r
Krot =½mr^2 ω^2 =½I ω^2
This formula also applies to lots of point masses or for extended objects such as rods or spheres.
EXAMPLE 1:
Consider two sticks, one twice as long as the other. They are initially held upright at the same angle as the vertical with their lower ends against the corner of the wall and floor. They are released at the same time. Which one hits the floor first?
The shorter one.
Explanation: This is a conservation of mechanical energy problem and rotational problem. The sticks are not free-falling, they are rotating. The longer stick starts with twice the gravitational potential energy – its CM is twice as high - but its moment of inertia is four times larger – I increase with the length squared. All the potential energy is converted to rotational kinetic energy just before the stick hits the floor. The larger the moment of inertia, the smaller ω must be to conserve energy.
EXAMPLE 2:
To make the longer stick fall faster and beat the short stick, you decide to add a mass equal to the weight of the stick at the end of the long stick Which stick hits the floor first? How does adding the weight affect the time it takes the long stick to fall?
The short stick hits the floor first. Adding the weight means the longer stick takes longer to fall than before.
Explanation: The added mass increased the initial potential energy but increased the moment of inertia by more. The larger moment of inertia means it rotates (falls) to the floor even slower than before.
EXAMPLE 3:
Can you add mass to the shorter stick so that the longer stick will win the race?
No: the shorter stick will always win no matter how much mass you add.
Rotational Work and Kinetic Energy
We previously defined the work done by a single force applied to an object as:
W=F×d
If the point where the force is applied rotates with the object and the torque is constant as the object rotates then
W_tor =τ×Δ θ
The work done by the torque changes the rotational kinetic energy according to the work energy principle.
work done by torque = change of rotational kinetic energy
W_tor =(K_rot ,final)−(Krot ,initial)
Angular Momentum
For fixed axis rotation we also introduce the angular equivalent of momentum – angular momentum.
If for linear motion:
p=mv
For fixed axis rotation we define the angular momentum L to be
L=I ω
For a point mass, I = mr^2 , and v = ω r, which gives
L=mr^2× v/r =m v r
Just as Newton’s 2nd Law was re-written in terms of momentum for linear motion, we can do the same for circular motion
change in angular momentum time interval =τnet
Conservation of Angular Momentum
If there is no net torque then the angular momentum is conserved
The total angular momentum of an object rotating around a fixed axis remains constant if the net external torque on it is zero
In equation form: if a and b are two times then
La =Lb
I_a(ω_a) =I_b(ω_b)
Many interesting phenomena can be understood as a consequence of the conservation of angular momentum.
Example: When the man pulls the weights inward, his rotational speed increases!

Translation and Rotation
So far the axis of rotation has been fixed.
Now we allow the axis to move in a direction perpendicular to the axis.
The motion of the object can be broken down into the translational motion of the axis and then the rotational motion of the object around the rotation axis.
For the case when the CM lies along the rotation axis:
The translational motion of the CM is governed by Newton’s 2nd Law using the net external force.
The rotational motion is given by the rotational form of Newton’s 2nd Law using the net external torque around the axis.
The net torque is not proportional to the net force.
A moving+rotating object has two forms of kinetic energy – translational and rotational. The total kinetic energy of an object with mass M is
Ktotal=Ktrans+ Krot
Ktotal=½ M vCM 2 +½I ω 2
I is the moment of inertia around the rotation axis.
For the case when the CM lies along the rotation axis:
The work done by the net external force changes the translational kinetic energy of the CM.
The work done by the net external torque around the rotation axis changes the rotational kinetic energy.
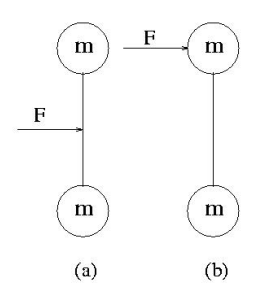
EX: A force is applied to a dumbbell for a certain time, first as in (a) and then as in (b). In which case does the dumbbell have more translational kinetic energy? In which case does the dumbbell have more total kinetic energy?
Rolling
Rolling is a combination of translation and rotation.
If an object rolls without slipping, the instantaneous point of contact between the surface and the object has zero velocity.
In most instances of rolling the CM lies along the rotation axis.
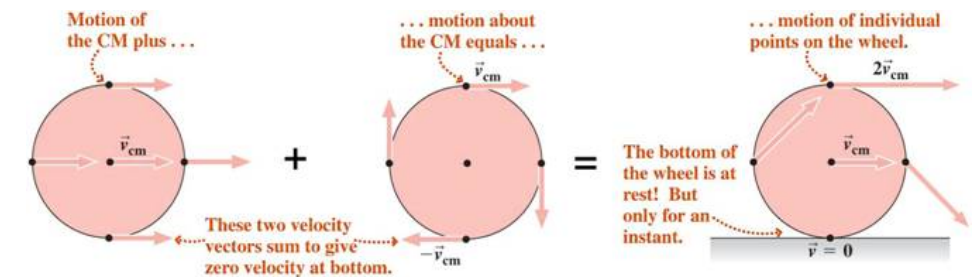
A rolling object has more kinetic energy than a point mass moving with the same CM speed.
The larger the moment of inertia, the larger the rotational kinetic energy for a given translational kinetic energy.
EX: A hoop and a disk are released from the top of an incline at the same time. Which one will reach the bottom first?
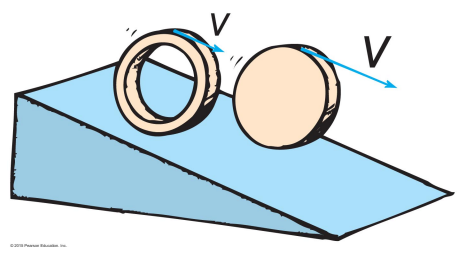
Disk

For both objects, their initial mechanical energy is just the gravitational potential energy.
At the bottom of the slope, the energy is all kinetic: some translational kinetic energy, some rotational.
The sum of the kinetic energies must equal the initial potential energy, but the object with the greater moment of inertia will have a greater proportion of rotational kinetic energy and thus less translational kinetic energy.
The smaller the translational kinetic energy, the smaller the speed of the CM.
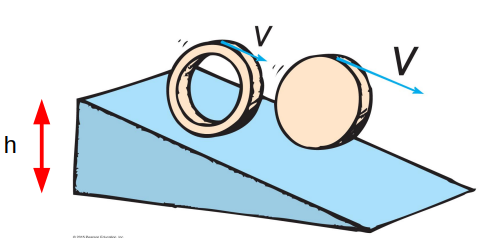
The object’s initial mechanical energy is just its gravitational potential energy
E_initial=mgh
At the bottom of the slope, its energy is all kinetic

Conserving mechanical energy and find the speed of the CM
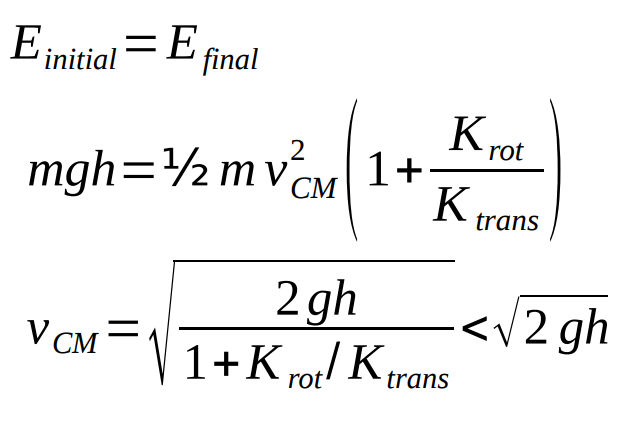
The larger then moment of inertia, the larger the ratio K_rot / K_trans and so the smaller the CM speed.
More of the gravitational potential energy went into rotational kinetic energy and less into translational kinetic energy.
PY 131 Chapter 8: Rotational Motion
Center of Mass
So far we have been treating all objects as point masses.
For every real object or system of objects, there is a point called the Center of Mass CM, which moves as if all the mass of the object were located there.
the CM does not have to be inside the object
Consider a system made from two point masses mA and mB placed along the x axis at xA and xB .
The total mass is
M=mA+ mB
The CM for the system is defined to be
x_CM = (m_A/M)(x_A) + (m_B/M)(x_B)
For a system of many point masses, x_CM is the weighted average of the x coordinate of each point mass.
This can be generalized to point masses, not along a line – the same formula applies to the y and z coordinates.
Consider three equal masses which form a triangle. The coordinates of the CM are the weighted average of their x and y coordinates.
Motion of the CM
Consider a system made up of two or more objects.
Their masses can all be different.
The total mass of all the objects is M.
The correct form for Newton’s Second Law is
a_CM = 1/M(F_ext)
Where Fext is the net external force on the system.
An external force is one that comes from something outside the system
If two objects in the system exert forces on each other, those are internal forces and do not contribute to Fext.
The center of mass moves like a point particle with mass M under the net external force acting on the system.
Rotational Motion
In addition to translational motion, objects which are not points, and systems of objects, can rotate.
We shall consider only rigid objects (rigid bodies) which have a fixed shape.
For now, the rotation is around a single line in space called the axis of rotation.

Polar Coordinates
Every point in the object moves in a circle.
Point P has coordinates x,y,z and is a distance r from the axis.
At time t the position vector makes an angle θ with the x axis.

Because the motion is circular the coordinates x and y are not very useful.
The more useful coordinates are the polar coordinates r and θ.
Angular Velocity
At time t_1 the angle is θ1 , at time t 2 the angle is θ2.
The average angular velocity ω is defined to be
ω¯= change in angle/change in time = (θ2−θ1)/(t 2−t 1) = Δθ/Δ t
The SI units of ω are radians/s (rad/s).
By convention, if ω is positive the rotation is counterclockwise (CCW), if it is negative the rotation is clockwise (CW).
When the time interval approaches zero the average angular velocity becomes the instantaneous angular velocity ω.
Period and Frequency
In one period T the object completes one revolution i.e. it rotates through 2π radians.
If the angular velocity is constant then ω = ω.
ω= Δ θ / Δ t = 2π / T
The frequency f is the inverse of the period T.
f = 1 / T
Angular Acceleration
At time t_1 the angular velocity is ω1 , at time t 2 the angular velocity is ω2.
The average angular acceleration α is defined to be
α¯= change in angular velocity / change in time = (ω2−ω1)/ (t 2−t 1) = Δ ω / Δt
The SI units of α are rad/s^2.
When the time interval approaches zero the average angular acceleration becomes the instantaneous angular acceleration α.
Any point in the object still has a linear (tangential) velocity, speed and acceleration.
The velocity vector always points along the tangent to the circle.
If the distance of the point is r from the axis then the linear speed is
v=r×ω
In a rigid object the tangential speed increases with distance from the axis of rotation.
The circumference of the circle grows but the period does not.
An object moving in a circle is accelerating.
The acceleration is related to the angular acceleration and angular velocity.
The general relation is complicated because in general there are two components of the acceleration.
One points towards the center and is called the centripetal acceleration aC
The centripetal acceleration causes the velocity to change direction only.
The other points in the same direction as the velocity (or opposite it) and is called the tangential acceleration, a_tan.
The tangential acceleration changes the size of the velocity (speed) only.
They are related to ω and α by the equations.
a_C=r×ω^2 = v^2/r
a_tan =r×α
In the special case where a_tan is zero, the acceleration points towards the center of the circle, and the object’s speed is constant.
This kind of motion is called uniform circular motion.

In general the acceleration points in a non-central direction. This kind of motion is called non-uniform circular motion.

Centripetal Force
The centripetal acceleration occurs due to the application of a force called the centripetal force.
Typically the force is a tension in a string, gravity, or a normal force, it is not some new force in the problem.
Since we know the centripetal acceleration, the force must be:
∑ _radial components F= FC=maC= mv^2 / r =mrω^2
The sum is over the radial components of the applied forces.
If an applied force has no radial component then it doesn't contribute.
If the component points towards the axis of rotation it is positive, away from the axis of rotation it is negative.

A rider on a Ferris wheel moves in a vertical circle of radius r at constant tangential speed v.
How does the normal force that the seat exerts on the rider change compared to the rider’s weight at the top and bottom of the wheel?
Another common instance of circular motion occurs when a car rounds a curved road.
The centripetal force – the force that causes the car to follow the curved road – is friction and/or the normal force if the road is banked.
if the wheels are not skidding then the point on the tire in contact with the ground is not moving plus the friction is perpendicular to the motion so the appropriate friction to use is static friction, not kinetic or rolling.
Centrifugal Force
In the frame of reference of an object moving in a circle, there is a force pushing on the object in the outward direction
This force is called the centrifugal force.
The centrifugal force is an example of a fictitious force – a force that is only felt in an accelerating frame of reference.
It is equal in size to the centripetal force.
The centrifugal force is why astronauts on the space station feel weightless – the centripetal force is their weight so in the frame of reference of the space station (which is also accelerating) the centrifugal force is equal and opposite their weight.
Torque
To make an object rotate – or change how it is rotating – we have to apply a force.
The larger the force the more rapidly the change in rotational motion of the object.
The effectiveness of the force increases with the distance from the axis of rotation.
The force is more effective if it is applied perpendicular to the vector from the axis to the point of application.

These observations indicate the relevant property is not force itself but the product of the size of the force, the distance from the rotation axis, and the angle the force is pointing.
This product is called the torque and usually represented by τ.
Torque is not exactly a vector but it has many properties of a vector e.g. it adds like all vectors do

If a torque tries to rotate an object in a CCW sense, it is positive.
If a torque tries to rotate an object CW it is negative.

Consider a force applied to an object which can rotate, at a particular point.
The force vector defines a line through space.
The lever arm is the shortest distance from the axis of rotation to that line.
The torque of the force is
τ=R⊥ F
The Moment of Inertia
The moment of inertia I plays the roll of mass for rotational motion.
The larger the moment of inertia the harder it is to change the angular velocity of a rotating object.
The moment of inertia for a point mass going around a circle with radius r is
I=mr^2

For a hoop, a disc and a sphere all of the same mass and radius, the moment of inertia of the hoop is largest, then the disc, then the sphere.
Newton’s Law of Fixed Axis Rotation
Newton's laws (in a modified form) also apply to fixed axis rotation.
Every object continues in its state of rest, or of uniform angular velocity, as long as no net torque acts on it.
The angular acceleration of an object about some axis is directly proportional to the net torque acting on it about that axis, and is inversely proportional to the object's moment of inertia I about that axis.
α= 1/I (τ_net)
Whenever one object exerts a torque on a second object, the second exerts an equal torque in the opposite direction on the first.
Kinetic Energy of Rotation
The kinetic energy of a single point mass is
Ktrans =½mv^2
If the point mass is going around in a circle of radius r
Krot =½mr^2 ω^2 =½I ω^2
This formula also applies to lots of point masses or for extended objects such as rods or spheres.
EXAMPLE 1:
Consider two sticks, one twice as long as the other. They are initially held upright at the same angle as the vertical with their lower ends against the corner of the wall and floor. They are released at the same time. Which one hits the floor first?
The shorter one.
Explanation: This is a conservation of mechanical energy problem and rotational problem. The sticks are not free-falling, they are rotating. The longer stick starts with twice the gravitational potential energy – its CM is twice as high - but its moment of inertia is four times larger – I increase with the length squared. All the potential energy is converted to rotational kinetic energy just before the stick hits the floor. The larger the moment of inertia, the smaller ω must be to conserve energy.
EXAMPLE 2:
To make the longer stick fall faster and beat the short stick, you decide to add a mass equal to the weight of the stick at the end of the long stick Which stick hits the floor first? How does adding the weight affect the time it takes the long stick to fall?
The short stick hits the floor first. Adding the weight means the longer stick takes longer to fall than before.
Explanation: The added mass increased the initial potential energy but increased the moment of inertia by more. The larger moment of inertia means it rotates (falls) to the floor even slower than before.
EXAMPLE 3:
Can you add mass to the shorter stick so that the longer stick will win the race?
No: the shorter stick will always win no matter how much mass you add.
Rotational Work and Kinetic Energy
We previously defined the work done by a single force applied to an object as:
W=F×d
If the point where the force is applied rotates with the object and the torque is constant as the object rotates then
W_tor =τ×Δ θ
The work done by the torque changes the rotational kinetic energy according to the work energy principle.
work done by torque = change of rotational kinetic energy
W_tor =(K_rot ,final)−(Krot ,initial)
Angular Momentum
For fixed axis rotation we also introduce the angular equivalent of momentum – angular momentum.
If for linear motion:
p=mv
For fixed axis rotation we define the angular momentum L to be
L=I ω
For a point mass, I = mr^2 , and v = ω r, which gives
L=mr^2× v/r =m v r
Just as Newton’s 2nd Law was re-written in terms of momentum for linear motion, we can do the same for circular motion
change in angular momentum time interval =τnet
Conservation of Angular Momentum
If there is no net torque then the angular momentum is conserved
The total angular momentum of an object rotating around a fixed axis remains constant if the net external torque on it is zero
In equation form: if a and b are two times then
La =Lb
I_a(ω_a) =I_b(ω_b)
Many interesting phenomena can be understood as a consequence of the conservation of angular momentum.
Example: When the man pulls the weights inward, his rotational speed increases!

Translation and Rotation
So far the axis of rotation has been fixed.
Now we allow the axis to move in a direction perpendicular to the axis.
The motion of the object can be broken down into the translational motion of the axis and then the rotational motion of the object around the rotation axis.
For the case when the CM lies along the rotation axis:
The translational motion of the CM is governed by Newton’s 2nd Law using the net external force.
The rotational motion is given by the rotational form of Newton’s 2nd Law using the net external torque around the axis.
The net torque is not proportional to the net force.
A moving+rotating object has two forms of kinetic energy – translational and rotational. The total kinetic energy of an object with mass M is
Ktotal=Ktrans+ Krot
Ktotal=½ M vCM 2 +½I ω 2
I is the moment of inertia around the rotation axis.
For the case when the CM lies along the rotation axis:
The work done by the net external force changes the translational kinetic energy of the CM.
The work done by the net external torque around the rotation axis changes the rotational kinetic energy.

EX: A force is applied to a dumbbell for a certain time, first as in (a) and then as in (b). In which case does the dumbbell have more translational kinetic energy? In which case does the dumbbell have more total kinetic energy?
Rolling
Rolling is a combination of translation and rotation.
If an object rolls without slipping, the instantaneous point of contact between the surface and the object has zero velocity.
In most instances of rolling the CM lies along the rotation axis.

A rolling object has more kinetic energy than a point mass moving with the same CM speed.
The larger the moment of inertia, the larger the rotational kinetic energy for a given translational kinetic energy.
EX: A hoop and a disk are released from the top of an incline at the same time. Which one will reach the bottom first?

Disk

For both objects, their initial mechanical energy is just the gravitational potential energy.
At the bottom of the slope, the energy is all kinetic: some translational kinetic energy, some rotational.
The sum of the kinetic energies must equal the initial potential energy, but the object with the greater moment of inertia will have a greater proportion of rotational kinetic energy and thus less translational kinetic energy.
The smaller the translational kinetic energy, the smaller the speed of the CM.

The object’s initial mechanical energy is just its gravitational potential energy
E_initial=mgh
At the bottom of the slope, its energy is all kinetic

Conserving mechanical energy and find the speed of the CM
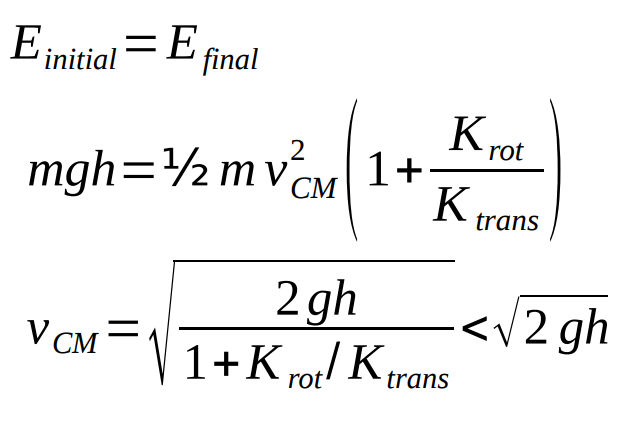
The larger then moment of inertia, the larger the ratio K_rot / K_trans and so the smaller the CM speed.
More of the gravitational potential energy went into rotational kinetic energy and less into translational kinetic energy.
 Knowt
Knowt
